Skip to main content

基于策略的算法（1）：Policy Gradient, REINFORCE

接下来我们进入另一个视角: 基于策略的算法

我们之前的算法都是基于值函数的，比如Q-learning，Sarsa等等。这些算法都是直接学习值函数，然后再通过值函数来选择动作。而基于策略的算法则是直接学习策略，然后再通过策略来选择动作。

基于值函数的哪里都挺好的，TD的方法也解决了大方差(未来的奖励依赖于未来的policy)的问题, 但基于值函数的算法有一个问题在于, 它选择策略需要计算所有的动作下的值函数, 再去取最大的。如果是离散的动作空间的话还好，但如果是连续的动作空间的话，这个计算量就太大了。

为了解决连续的动作空间的问题, 我们还是仿照之前的思路, 用一个神经网络来拟合策略。这个神经网络的输入是状态, 输出是动作的概率分布。这样我们就可以直接从这个概率分布中采样出动作。就引出了所谓"基于策略"的算法。对策略函数使用梯度上升的方法，使得策略函数的期望回报最大化。

但这里又绕回到原来那个问题, 策略决定未来的reward, 叠加起来导致方差太大, 不利于训练, 因而我们有许多种解决方案:

  • 用基线(baseline)减小方差 -> REINFORCE with baseline
  • 限制策略的改变量 -> TRPO, PPO, ...

但即使有这些方法, 它的方差还是比较大, 是不能和value-based的方法比的, 因此引出了将policy-based和value-based结合的Actor-Critic系列算法，具体来说是用value-based算法当actor学到的东西作为policy算法（critic）的梯度更新参数

Policy Gradient​

还是拿马里奥举例, 我们把策略函数用神经网络建模, 其架构大致如下:

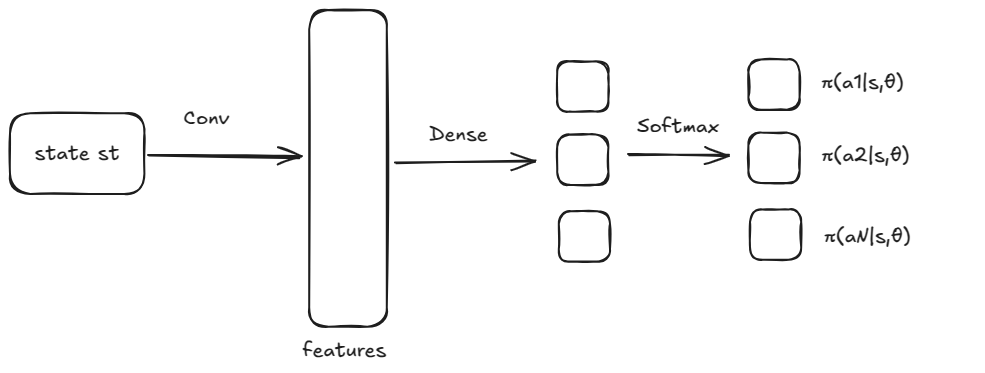
image-20250211215506573

我们想要优化的是神经网络的参数θ, 如何设计优化目标?

Vπ(st)→V(s;θ)V_{\pi}(s_t) \to V(s;\theta), 我们只需要消去s即可，也是经典的用期望的手法

J(θ)=ES(V(S;θ)),\partV(s;θ)\partθ=∂∂θ∑aπ(a∣s,θ)Qπθ(s,a)J(\theta) = E_S(V(S;\theta)), \frac{\part V(s;\theta)}{\part \theta}=\frac{\partial}{\partial \theta }\sum_a \pi(a|s, \theta)Q_{\pi_{\theta}}(s,a)

这个导数作用在乘积上, 但我们可以假装它只作用在第一项π\pi上, 可以证明第二项q上的结果和第一项上成线性关系, 这部分实际上可以通过调节学习率来抵消掉

于是∂∂θ∑aπ(a∣s;θ)Qπθ(s,a)∝∑a∂∂θπ(a∣s;θ)Qπθ(s,a)=∑aπ(a∣s;θ)∂lnπ(a∣s;θ)∂θQπ(s,a)=EA∼π(⋅∣s,θ)[∂lnπ(a∣s;θ)∂θQπ(s,a)]\frac{\partial}{\partial \theta }\sum_a \pi(a|s;\theta)Q_{\pi_{\theta}}(s,a) \propto \sum_a \frac{\partial}{\partial \theta }\pi(a|s;\theta)Q_{\pi_{\theta}}(s,a) = \sum_a \pi(a|s;\theta) \frac{\partial ln\pi(a|s;\theta)}{\partial \theta}Q_{\pi}(s,a) = E_{A \sim \pi(\cdot|s, \theta)}[\frac{\partial ln\pi(a|s;\theta)}{\partial \theta}Q_{\pi}(s,a)]

更新θ\theta的公式就是: θ←θ+β∇θJ(θ)\theta \leftarrow \theta + \beta \nabla_{\theta}J(\theta)

最后的式子很重要, 它告诉我们朴素的policy gradient是一个on-policy算法, 必须让A∼π(⋅∣s,θ)A\sim \pi(\cdot|s,\theta)这样的动作空间,即用最新的策略网络采样出来的动作才能用于计算梯度

如果动作空间是离散的, 那我们可以用倒数第二项，但连续的就只能用这个期望的形式了

剩下还有一个问题是, Qπ(s,a)Q_{\pi}(s,a)这个东西怎么计算呢? 我们可以用MC的方法, 也就是用一个episode的reward来估计这个值

这样的就是policy gradient的算法了, policy gradient with MC就是REINFORCE算法, 用采样ut=∑k=tTrku_t = \sum_{k=t}^{T}r_k来估计Qπ(st,at)Q_{\pi}(s_t,a_t)后带入上面的公式就能计算出梯度了

一个典型的代码可能长这样

import torch
import torch.nn as nn
import torch.optim as optim
import gym

# 定义策略网络
class PolicyNetwork(nn.Module):
    def __init__(self, state_dim, action_dim):
        super(PolicyNetwork, self).__init__()
        self.fc1 = nn.Linear(state_dim, 128)
        self.fc2 = nn.Linear(128, action_dim)

    def forward(self, x):
        x = torch.relu(self.fc1(x))
        x = torch.softmax(self.fc2(x), dim=-1)  # 使用softmax确保概率输出
        return x

    def act(self, state):
        probs = self.forward(state)
        dist = torch.distributions.Categorical(probs)
        action = dist.sample()
        return action, dist.log_prob(action)


# 超参数
learning_rate = 0.001
gamma = 0.99
num_episodes = 1000

# 创建环境
env = gym.make("CartPole-v1")
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.n

# 实例化策略网络和优化器
policy_net = PolicyNetwork(state_dim, action_dim)
optimizer = optim.Adam(policy_net.parameters(), lr=learning_rate)

# 训练循环
for episode in range(num_episodes):
    state = env.reset()[0]
    state = torch.tensor(state, dtype=torch.float32)
    episode_rewards = []
    log_probs = []

    done = False
    while not done:
        action, log_prob = policy_net.act(state.unsqueeze(0)) # unsqueeze(0) 添加batch维度
        next_state, reward, terminated, truncated, _ = env.step(action.item())
        done = terminated or truncated

        episode_rewards.append(reward)
        log_probs.append(log_prob)
        state = torch.tensor(next_state, dtype=torch.float32)

    # 计算回报
    returns = []
    R = 0
    for r in episode_rewards[::-1]:
        R = r + gamma * R
        returns.insert(0, R)
    returns = torch.tensor(returns, dtype=torch.float32)

    # 计算损失
    loss = -torch.sum(torch.stack(log_probs) * returns)

    # 更新参数
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    print(f"Episode: {episode+1}, Total Reward: {sum(episode_rewards)}, Loss: {loss.item()}")

env.close()

REINFORCE算法的缺点很显然: MC+Policy-based方差太大, 很难收敛

一个重要的优化是引入baseline, 也就是减去一个基线值, 使得方差减小

我们研究上面的导数项:

EA∼π(⋅∣s,θ)[∂lnπ(a∣s;θ)∂θQπ(s,a)]E_{A \sim \pi(\cdot|s, \theta)}[\frac{\partial ln\pi(a|s;\theta)}{\partial \theta}Q_{\pi}(s,a)], 发现可以在后面加上一个与θ\theta无关的函数b(s)b(s), 导出来是0不影响结果

但期望没变, 方差可以减小, 理论计算可以得到一个最优的b(s), 它近似等于Vπ(s)V_{\pi}(s), 也就是状态s的value函数

那么问题又来了, 如何得到Vπ(s)V_{\pi}(s)?

注意policy-gradient是on-policy的,不再能多次采样取平均得到VV了

那我们只能用一个神经网络拟合V(s,θ)V(s,\theta)，然后用采样的trajectory reward和它的值的MSE作为Loss更新这个网络

有点像后续的Actor-Critic算法了,但区别在于V(s,θ)V(s,\theta)算法并不评价policy，两个网络都是由MC采样来评价的, 这个就是REINFORCE with baseline算法

import torch
import torch.nn as nn
import torch.optim as optim
import gym

# 定义策略网络
class PolicyNetwork(nn.Module):
    # ... (与之前代码相同) ...

# 定义值网络
class ValueNetwork(nn.Module):
    def __init__(self, state_dim):
        super(ValueNetwork, self).__init__()
        self.fc1 = nn.Linear(state_dim, 128)
        self.fc2 = nn.Linear(128, 1)

    def forward(self, x):
        x = torch.relu(self.fc1(x))
        x = self.fc2(x)
        return x


# 超参数
learning_rate = 0.001
gamma = 0.99
num_episodes = 1000

# 创建环境
env = gym.make("CartPole-v1")
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.n

# 实例化策略网络、值网络和优化器
policy_net = PolicyNetwork(state_dim, action_dim)
value_net = ValueNetwork(state_dim)
optimizer_policy = optim.Adam(policy_net.parameters(), lr=learning_rate)
optimizer_value = optim.Adam(value_net.parameters(), lr=learning_rate)

# 训练循环
for episode in range(num_episodes):
    state = env.reset()[0]
    state = torch.tensor(state, dtype=torch.float32)
    episode_rewards = []
    log_probs = []
    states = []

    done = False
    while not done:
        action, log_prob = policy_net.act(state.unsqueeze(0))
        next_state, reward, terminated, truncated, _ = env.step(action.item())
        done = terminated or truncated

        episode_rewards.append(reward)
        log_probs.append(log_prob)
        states.append(state)
        state = torch.tensor(next_state, dtype=torch.float32)

    # 计算回报
    returns = []
    R = 0
    for r in episode_rewards[::-1]:
        R = r + gamma * R
        returns.insert(0, R)
    returns = torch.tensor(returns, dtype=torch.float32)

    # 计算状态值
    states = torch.stack(states)
    values = value_net(states).squeeze(-1)

    # 计算优势函数
    advantages = returns - values

    # 计算损失
    loss_policy = -torch.sum(torch.stack(log_probs) * advantages)
    loss_value = nn.MSELoss()(values, returns) # 均方误差损失

    # 更新参数
    optimizer_policy.zero_grad()
    loss_policy.backward()
    optimizer_policy.step()

    optimizer_value.zero_grad()
    loss_value.backward()
    optimizer_value.step()

    print(f"Episode: {episode+1}, Total Reward: {sum(episode_rewards)}, Policy Loss: {loss_policy.item()}, Value Loss: {loss_value.item()}")

env.close()